Cardioid!
What is a Cardioid anyway? Well, it's this fat bean shaped thing apparently looks like a heart.
"What's so important about this?", you ask. Well, it's just like the Fibonacci sequence, it appears everywhere without you even noticing. For example, sunlight in a mug, in a bowl. The shape of the Mandelbrot Set...
"What's so important about this?", you ask. Well, it's just like the Fibonacci sequence, it appears everywhere without you even noticing. For example, sunlight in a mug, in a bowl. The shape of the Mandelbrot Set...
Hmm, isn't that weird? Let's make more of these.
One way we can make this is by connecting dots on a circle. First, pick two random points on the circle's edge, and then connect them with a straight line. Then, pick the next two points by simply moving one of the points a certain distance clockwise (counter clockwise would work too) on the circle, while moving the other point twice the distance you did the first point. Connect the two new point with a straight line and repeat. This is what it'll look like eventually when you go around the whole circle:
One way we can make this is by connecting dots on a circle. First, pick two random points on the circle's edge, and then connect them with a straight line. Then, pick the next two points by simply moving one of the points a certain distance clockwise (counter clockwise would work too) on the circle, while moving the other point twice the distance you did the first point. Connect the two new point with a straight line and repeat. This is what it'll look like eventually when you go around the whole circle:
Note that one of the points moved around the circle twice as fast (therefore went around the circle twice) while the other point only moved around once.
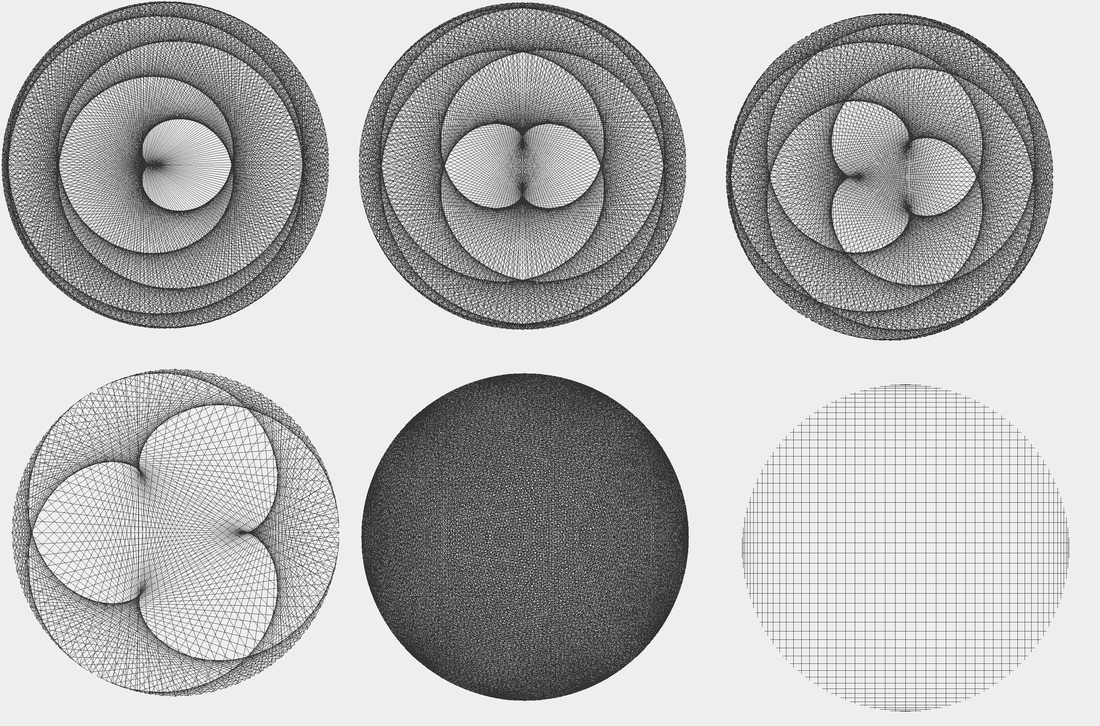
Now you're probably wondering, what would the shape be if one of the points moved three times as fast as the other? four times?!?
Well, let's see:
Now you're probably wondering, what would the shape be if one of the points moved three times as fast as the other? four times?!?
Well, let's see:
Can you guess which one is which? Hint: Top left is 3 times.
Now this is definitely cool. Of course you don't want to waste time connecting dots, but you want to see more shapes... so.. we write an algorithm that draws it for us!
Now this is definitely cool. Of course you don't want to waste time connecting dots, but you want to see more shapes... so.. we write an algorithm that draws it for us!
A simple few lines of code would do it. Let me explain some of the variables used here:
I made an executable JAR file so you can play around and see what shapes you get with different multipliers. If you're java savvy, feel free to mess around the code and make more cool shapes!
- order and totalorder: the number of lines you want to draw.
- count: this is responsible for moving the points around the circle. The bigger the count, the more it'll move.
- mult: multiplier. Yes, it's how fast one point should move relative to the other. You'll get the normal Cardioid if mult = 2
I made an executable JAR file so you can play around and see what shapes you get with different multipliers. If you're java savvy, feel free to mess around the code and make more cool shapes!
|
| ||||||||||||
The program won't work very well if you have a tiny screen... Sorry... as in, sorry for your tiny screen.
Anyway, simply enter the multiplier in the top-left box and press enter. The program would draw the circle for you :).
Notice how the multiplier is initially set to 1, which means that it'll just draw a circle, with dots. It's there, just very faint.
The multiplier doesn't have to be a whole number! Try with other cool numbers and see what you get.
Have fun!
Last Updated: 4 April 2015
Anyway, simply enter the multiplier in the top-left box and press enter. The program would draw the circle for you :).
Notice how the multiplier is initially set to 1, which means that it'll just draw a circle, with dots. It's there, just very faint.
The multiplier doesn't have to be a whole number! Try with other cool numbers and see what you get.
Have fun!
Last Updated: 4 April 2015