Dots and Boxes
Dots and Boxes (also called Boxes, Squares, Paddocks, Pigs in a Pen, Square-it, Dots and Dashes, Dots, Line Game, Smart Dots, Dot Boxing, or, simply, the Dot Game) is a simple game where players try to "claim" as many boxes as possible by drawing lines connecting the dots on the paper. Starting with an empty grid of dots, players take turns, adding a single horizontal or vertical line between two unjoined adjacent dots. A player who completes the fourth side of a 1×1 box earns one point and takes another turn. (The points are typically recorded by placing in the box an identifying mark of the player, such as an initial). The game ends when no more lines can be placed. The winner of the game is the player with the most points (Source). This game is first published by Édouard Lucas (he also invented the Tower of Hanoi puzzle).
I actually never learned how to play the game until I watched a NumberPhile video about it a few months ago:
I actually never learned how to play the game until I watched a NumberPhile video about it a few months ago:
tl;dw (too long; didn't watch): The video explained a few strategies on playing the game with 4x4 dots, or 3x3 squares. What I'm interested is, are these strategies actually correct? Are they actually efficient?
To find out, I need to write a program that 'solves' the game for me. But before I do that, I need to program the game itself. A couple of questions arise:
1) How to keep track of edges efficiently?
2) How to keep track of boxes that aren't claimed, but they have edges already?
3) How do I check if a move is valid?
4) What is the most efficient way of storing a move?
Things become more complicated when you think about how an edge is actually a side of, possibly, two boxes.
Boxes share edges in this game.
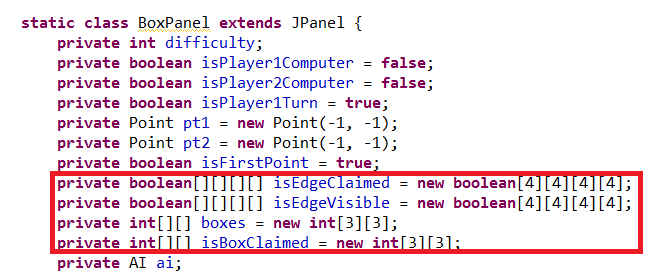
So what did I do instead? I ended up adopting a coordinate system for the dots. As I was programming, I also realized that there is no need to store information on which edges are owned by which player - simply whether the edge was claimed or not was enough. I used an incredibly memory wasting 4D array of booleans to store whether an edge was claimed or not: boolean[][][][] isEdgeClaimed = new boolean[4][4][4][4]; // The four dimensions are organized like so: [pt1.x][pt1.y][pt2.x][pt2.y]
Using the idea that two points define a line, this 4D array can potentially define any line between any two points on the grid, in both directions. Since we only need the sides of the square, I set everything unnecessary to 'false', meaning that they are already claimed, and cannot be claimed even if you tried.
For the boxes, I used a 2D integer array to store whether the box is claimed, and by which player. If an element is a 0, that means the box is not claimed, 1 means it's claimed by player 1, and 2 means it's claimed by player 2. Simple enough: int[][] isBoxClaimed = new int[3][3];
Finally, I used another 2D array to store how many sides each box already have completed (with 4 being completed...etc.). This turned out to be easier to implement than I thought, because it is actually unnecessary to store which specific sides each box have and don't have. 'How many sides are completed' will do: int[][] boxes = new int[3][3]; And of course, a box with 4 sides completed means the box is completely enclosed, and the player then should claim that box...etc.
So now my declaration looks like this:
To find out, I need to write a program that 'solves' the game for me. But before I do that, I need to program the game itself. A couple of questions arise:
1) How to keep track of edges efficiently?
2) How to keep track of boxes that aren't claimed, but they have edges already?
3) How do I check if a move is valid?
4) What is the most efficient way of storing a move?
Things become more complicated when you think about how an edge is actually a side of, possibly, two boxes.
Boxes share edges in this game.
So what did I do instead? I ended up adopting a coordinate system for the dots. As I was programming, I also realized that there is no need to store information on which edges are owned by which player - simply whether the edge was claimed or not was enough. I used an incredibly memory wasting 4D array of booleans to store whether an edge was claimed or not: boolean[][][][] isEdgeClaimed = new boolean[4][4][4][4]; // The four dimensions are organized like so: [pt1.x][pt1.y][pt2.x][pt2.y]
Using the idea that two points define a line, this 4D array can potentially define any line between any two points on the grid, in both directions. Since we only need the sides of the square, I set everything unnecessary to 'false', meaning that they are already claimed, and cannot be claimed even if you tried.
For the boxes, I used a 2D integer array to store whether the box is claimed, and by which player. If an element is a 0, that means the box is not claimed, 1 means it's claimed by player 1, and 2 means it's claimed by player 2. Simple enough: int[][] isBoxClaimed = new int[3][3];
Finally, I used another 2D array to store how many sides each box already have completed (with 4 being completed...etc.). This turned out to be easier to implement than I thought, because it is actually unnecessary to store which specific sides each box have and don't have. 'How many sides are completed' will do: int[][] boxes = new int[3][3]; And of course, a box with 4 sides completed means the box is completely enclosed, and the player then should claim that box...etc.
So now my declaration looks like this:
The ones in the red box are the ones that are important to the game. isEdgeVisisble isn't that important, really; it's just for the ease of displaying the correct edges on the JApplet everytime I repaint the screen. I might explain the rest of the variables later. But I do think very far ahead when programming - I make all the variables I might need, even though they do nothing as of now.
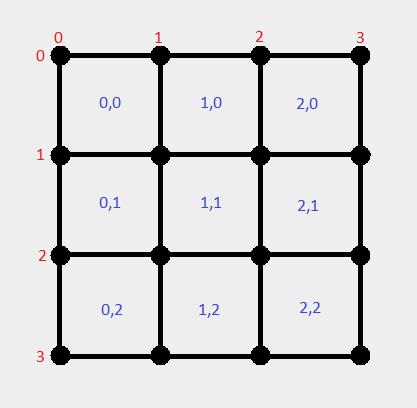
Anyway, my gameplay "board" is basically organized like this:
Anyway, my gameplay "board" is basically organized like this:
The red coordinates are for the dots, the blue coordinates are for the boxes.
Now, the last part to make this game playable (not including displaying/painting the board, because that's weird stuff) - is to use the data variables we just initialized. Given a valid input, or two adjacent points: Point pt1 = new Point(x1, y1); and Point pt2 = new Point(x2, y2);, how do we update the game state appropriately? We immediately encounter a problem: these edges have direction! (0,0), (0,1) and (0,1), (0,0) are effectively 'different' edges in our data system.
Now, the last part to make this game playable (not including displaying/painting the board, because that's weird stuff) - is to use the data variables we just initialized. Given a valid input, or two adjacent points: Point pt1 = new Point(x1, y1); and Point pt2 = new Point(x2, y2);, how do we update the game state appropriately? We immediately encounter a problem: these edges have direction! (0,0), (0,1) and (0,1), (0,0) are effectively 'different' edges in our data system.
|
An easy way to solve this would be forcing the first point to have a 'lower value' compared to the second point - as in, the first point is nearer to the origin than the second. Using this method, we would have an uniform coordinate system - effectively eliminating one of the directions for each edge.
This is easy to do, as shown by the code on the left. Simply swap the points if any of the values of the first point is larger than the second's. |
Having this, we can now continue to think about updating the game 'state' given a valid move. Here are some things to think about:
1) Each edge is part of at least one box. Which edges are part of two different boxes?
2) How do I identify which boxes each edge belongs to?
3) What happens when a box has all its edges claimed?
Here is the code I came up with, given pt1 and pt2 are the inputs:
1) Each edge is part of at least one box. Which edges are part of two different boxes?
2) How do I identify which boxes each edge belongs to?
3) What happens when a box has all its edges claimed?
Here is the code I came up with, given pt1 and pt2 are the inputs:
- Line 202 checks if the move/edge is claimed and valid. If a move is not valid, our boolean 4D array would return that the edge is "claimed" already.
- Line 203: the boolean variable is made for the fact that if a user claims a box, he gets to take another turn. You can see in line 237 I only swap players if there is not a newBoxClaim-ed.
- isPlayer1Turn is a boolean variable that stores whether player 1 is playing or player 2.
- Lines 204-205: claims the valid edge by updating the data structure with the current move.
- Lines 206 and 221 effectively separate the two fundamental types of edges: vertical or horizontal.
- Lines 207, 214, 222, 229 checks if the edge is on the side of the board or not. Because if an edge is on the side of the board, it's only part of one box.
- Lines 209, 216, 224, 231 checks if a box has four edges already, and if it does, we store which player owns that box in the variable "isBoxClaimed".
- getPlayerNumber() returns a 1 if player1 is playing, 2 if player2 is playing.
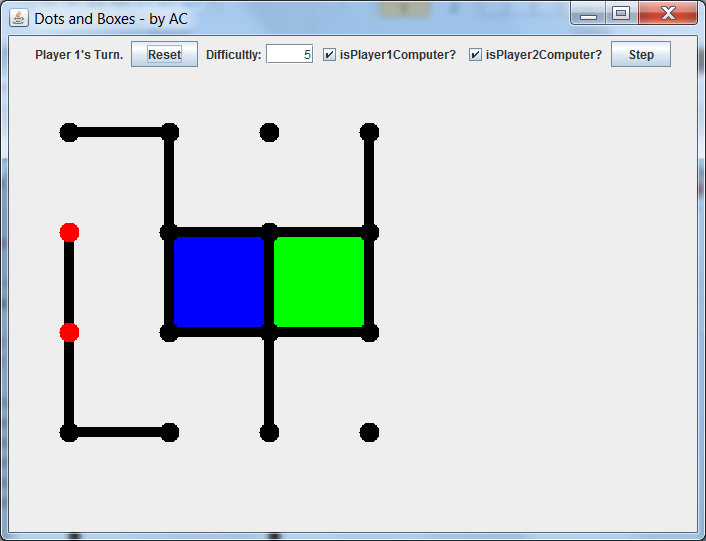
That's it! That's all you need to make a playable dots and boxes game. Well, at least the data structure and the logic is there; all you need to do is output the game state somehow so you can see it. But I won't go into detail on how to do that, since it's something that each person does differently. Here is a screenshot and a runable JAR for dots and boxes without the AI (which I'll talk about later). Yes, those extra buttons do nothing.
| |||||||
Last Updated: 30 May, 2015
A.I.
Warning: This is the first substantial A.I. I've ever coded, so...
Before I started coding, I made a rough list of goals I want to meet with this A.I.
With that settled, it's time to start! The basic idea is that, there is a finite number of game states (knowing that there're finite number of moves), so it is not a bad idea to look at all the possible moves and pick the best one out of those moves. It just sounds too good to be true: all we need to do is find all the possible moves by us and by our opponent, put it in a tree, and perhaps choose each move based on the proportion of winning games out of all possible game states.
Turns just 24 different possibilities is still too much for the computer to handle... It's only just 24 Factorial + 23 Factorial + 22 Factorial + 21 Factorial + .... + 3 Factorial + 2 Factorial + 1 number of states! Turns out that's a huge number:
--To be continued--
Before I started coding, I made a rough list of goals I want to meet with this A.I.
- Operate without specific strategies or instructions hard-coded.
- Fully Adjustable.
- Fast making decisions.
- Relatively unpredictable
With that settled, it's time to start! The basic idea is that, there is a finite number of game states (knowing that there're finite number of moves), so it is not a bad idea to look at all the possible moves and pick the best one out of those moves. It just sounds too good to be true: all we need to do is find all the possible moves by us and by our opponent, put it in a tree, and perhaps choose each move based on the proportion of winning games out of all possible game states.
Turns just 24 different possibilities is still too much for the computer to handle... It's only just 24 Factorial + 23 Factorial + 22 Factorial + 21 Factorial + .... + 3 Factorial + 2 Factorial + 1 number of states! Turns out that's a huge number:
--To be continued--